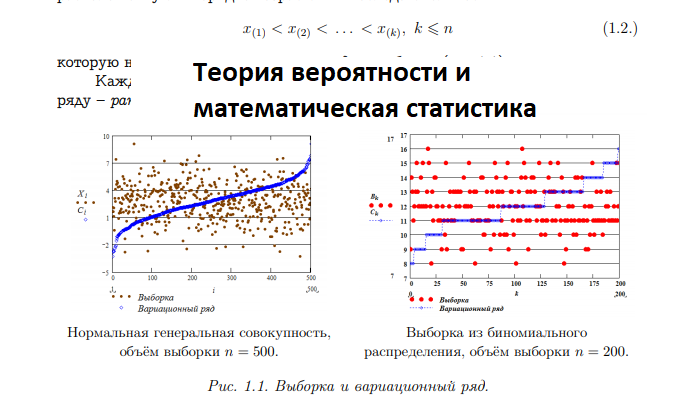
В курсе «Теория вероятности и математическая статистика» раскрываются основные понятия теории вероятностей и математической статистики. Особое внимание уделяется основным положениям и методам современной математической теории вероятностей, приложениям теории – в физике, экологии, экономике и статистике. Знания, полученные в курсе, помогут приобрести навыки в интерпретации теоретико-вероятностных конструкций внутри математики и за ее пределами в приложениях, решении проблемных теоретико-вероятностных задач.
Целью изучения курса «Теория вероятности и математическая статистика» является формирование знаний студентов в области основ математических и естественнонаучных дисциплин, формирование знаний о теории вероятностей, как особом способе познания мира и образе мышления, изучение основ статистического описания данных, постановок и методов решения задач математической статистики, таких как задачи статистического оценивания и проверки гипотез, изучение основ анализа статистических зависимостей
- Владелец: ТОО SYSTEMS-S
В результате освоения дисциплины студент должен:
знать:
- место курса среди других изучаемых дисциплин и его значение при изучении последующих курсов;
- основы теории дифференциальных уравнений;
- теорию числовых и функциональных рядов;
- теорию функций комплексного переменного;
- основы операционного метода
уметь:
- решать дифференциальные уравнения первого и второго порядков, находить их общее и частные решения;
- решать системы обыкновенных дифференциальных уравнений;
- исследовать на сходимость знакоположительные числовые ряды;
- исследовать на абсолютную и условную сходимость знакопчередующиеся числовые ряды;
- находить интервалы сходимости степенных рядов;
- представлять функцию степенным рядом;
- применять ряды в приближенных вычислениях;
- выполнять действия с комплексными числами в различных формах записи, переходить одной формы представления комплексного числа к другой;
- вычислять значения функций комплексного переменного, выделять действительную и мнимую часть выражения;
- находить производные и интегралы от функций комплексного переменного;
- находить оригиналы и изображения, находить частные решения линейных дифференциальных уравнений и систем операционным методом;
- работать с учебной и справочной литературой;
- применять методы, изученные в курсе «Математика 3.1», к решению инженерных, исследовательских и других профессиональных задач;
- использовать полученные знания при усвоении учебного материала последующих дисциплин.
владеть:
- математической символикой для выражения количественных и качественных отношений объектов,
- методами построения простейших математических моделей типовых профессиональных задач,
- математическими методами решения естественнонаучных задач и методами интерпретации полученных результатов,
- математическим аппаратом для описания, анализа, теоретического и экспериментального исследования и моделирования физических и электрических систем, явлений и процессов, приемами использования математического аппарата в обучении и профессиональной деятельности.

- Владелец: ТОО SYSTEMS-S
В результате освоения дисциплины студент должен:
знать:
- место курса среди других изучаемых дисциплин и его значение при изучении последующих курсов;
- основы интегрального исчисления;
- теорию числовых и функциональных рядов;
- основы теории дифференциальных уравнений.
уметь:
- решать задачи геометрического и физического характера с помощью интегрального исчисления;
- решать дифференциальные уравнения первого и второго порядков, находить их общее и частные решения;
- решать системы обыкновенных дифференциальных уравнений;
- представлять функцию степенным рядом;
- вычислять с помощью степенных рядов интегралы и решать дифференциальные уравнения;
- работать с учебной и справочной литературой;
- применять методы, изученные в курсе «Математика 2.3», к решению инженерных, исследовательских и других профессиональных задач;
- использовать полученные знания при усвоении учебного материала последующих дисциплин.
владеть:
- математической символикой для выражения количественных и качественных отношений объектов,
- методами построения простейших математических моделей типовых профессиональных задач,
- математическими методами решения естественнонаучных задач и методами интерпретации полученных результатов,
- математическим аппаратом для описания, анализа, теоретического и экспериментального исследования и моделирования физических и химических систем, явлений и процессов, приемами использования математического аппарата в обучении и профессиональной деятельности.

- Владелец: ТОО SYSTEMS-S
Содержание дисциплины
- Элементы линейной алгебры;
- Векторная алгебра;
- Аналитическая геометрия;
- Элементы теории линейных пространств и линейных операторов.
В результате освоения дисциплины студент должен
знать:
- основы линейной алгебры, векторной алгебры, аналитической геометрии, теории линейных операторов;
уметь:
- решать системы линейных уравнений;
- выполнять линейные и нелинейные операции над векторами;
- строить алгебраические кривые и поверхности, Задавать их аналитически;
- находить матрицу линейного оператора, ее собственные значения и векторы;
владеть
- методами линейной алгебры и аналитической геометрии.

- Владелец: ТОО SYSTEMS-S
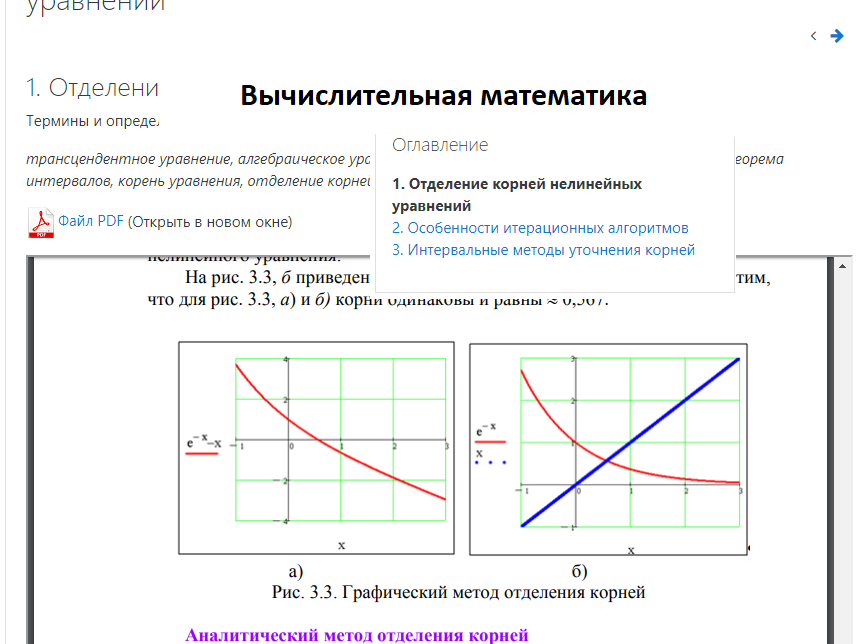
Дисциплина «Вычислительная математика» изучается студентами 2-го курса основной образовательной программы подготовки бакалавров по направлению 09.03.01 «Информатика и вычислительная техника».
Курс предназначен для изучения методов и алгоритмов численного решения основных математических и инженерных задач.
Основное внимание уделяется пониманию отличия численного решения от аналитического, оценке погрешности численного решения, вопросам сходимости и устойчивости алгоритмов и методов.
Каждый раздел излагается в общей концепции: содержательная – формализованная постановка задачи – методы ее решения и условия их применения – алгоритмизация методов – оценка погрешностей решения и эффективности алгоритмов.
В результате обучения по данному курсу студент будет способен:
Осуществлять переход от содержательной постановки инженерной задачи к формализованному описанию.
Осуществлять выбор методов решения и формирование требований к задаче вычислительной математики.
Разрабатывать алгоритмы и программы получения численного решения задачи вычислительной математики.
Оценивать погрешности численного решения и эффективность алгоритма.
- Владелец: ТОО SYSTEMS-S
Электронный курс «Дискретная математика» разработан исходя из следующих, сформулированных в Основной образовательной программе по направлению 15.03.04 «Автоматизация технологических процессов и производств», планируемых результатов обучения:
- знать место и роль дискретной математики в современном мире,
- уметь сформулировать задачу исследований дискретного объекта, используя теоретико-множественные, логические и графические средства конструктивного анализа и моделирования,
- уметь переходить от одной формы математического представления дискретной модели к другой,
- владеть навыками и методами построения моделей дискретных объектов автоматизации и управления.
- знать приложения изучаемого материала в других разделах математики.

- Владелец: ТОО SYSTEMS-S